
Estimating the entropy of neural data by saving them as a .png file
 and Fleur Zeldenrust based on reviews by Federico Stella and 2 anonymous reviewers
and Fleur Zeldenrust based on reviews by Federico Stella and 2 anonymous reviewers
A quick and easy way to estimate entropy and mutual information for neuroscience
Abstract
Recommendation: posted 20 April 2021, validated 20 April 2021
Olafsdottir, H., Karnani, M. and Zeldenrust, F. (2021) Estimating the entropy of neural data by saving them as a .png file. Peer Community in Neuroscience, 100001. 10.24072/pci.cneuro.100001
Recommendation
Entropy and mutual information are useful metrics for quantitative analyses of various signals across the sciences including neuroscience (Verdú, 2019). The information that a neuron transfers about a sensory stimulus is just one of many examples of this. However, estimating the entropy of neural data is often difficult due to limited sampling (Tovée et al., 1993; Treves and Panzeri, 1995). This manuscript overcomes this problem with a 'quick and dirty' trick: just save the corresponding plots as PNG files and measure the file sizes! The idea is that the size of the PNG file obtained by saving a particular set of data will reflect the amount of variability present in the data and will therefore provide an indirect estimation of the entropy content of the data.
The method the study employs is based on Shannon’s Source Coding Theorem - an approach used in the field of compressed sensing - which is still not widely used in neuroscience. The resulting algorithm is very straightforward, essentially consisting of just saving a figure of your data as a PNG file. Therefore it provides a useful tool for a fast and computationally efficient evaluation of the information content of a signal, without having to resort to more math-heavy methods (as the computation is done “for free” by the PNG compression software). It also opens up the possibility to pursue a similar strategy with other (than PNG) image compression software. The main limitation is that the PNG conversion method presented here allows only a relative entropy estimation: the size of the file is not the absolute value of entropy, due to the fact that the PNG algorithm also involves filtering for 2D images.
The study comprehensively reviews the use of entropy estimation in circuit neuroscience, and then tests the PNG method against other math-heavy methods, which have also been made accessible elsewhere (Ince et al., 2010). The study demonstrates use of the method in several applications. First, the mutual information between stimulus and neural response in whole-cell and unit recordings is estimated. Second, the study applies the method to experimental situations with less experimental control - such as recordings of hippocampal place cells (O’Keefe & Dostrovsky,1971) as animals freely explore an environment. The study shows the method can replicate previously established metrics in the field (e.g. Skaggs information, Skaggs et al. 1993). Importantly, it does this while making fewer assumptions on the data than traditional methods. Third, he study extends the use of the method to imaging data of neuronal morphology, such as charting the growth stage of neuronal cultures. However, the radial entropy of a dendritic tree seems at first more difficult to interpret than the common Sholl analysis of radial crossings of dendrite segments (Figure 6Ac of Zbili and Rama, 2021). As the authors note, a similar technique is used in paleobiology to discriminate pictures of biogenic rocks from abiogenic ones (Wagstaff and Corsetti, 2010). Perhaps neuronal subtypes could also be easily distinguished through PNG file size (Yuste et al., 2020). These examples are generally promising and creative applications.The authors used open source software and openly shared their code so anyone can give it a spin (https://github.com/Sylvain-Deposit/PNG-Entropy).
We were inspired by the wide applicability of the presented back-of-the-envelope technique, so we used it in a situation that the study had not tested: namely, the dissection of microcircuits via optogenetic tagging of target neurons. In this process, one is often confronted with the problem that not only the opsin-carrying cells will spike in response to light, but also other nearby neurons which are activated synaptically (via the opto-tagged cell). Separating these two types of responses is typically done using a latency or jitter analysis, which requires the experimenter subjectively searching for detection parameters. Therefore a rapid and objective technique is preferable. The PNG rate difference method on slice whole cell recordings of opsin tagged neurons revealed higher mutual information metrics for direct optogenetic activation than for postsynaptic responses, showing the method can be easily used to objectively segregate different spike triggers.
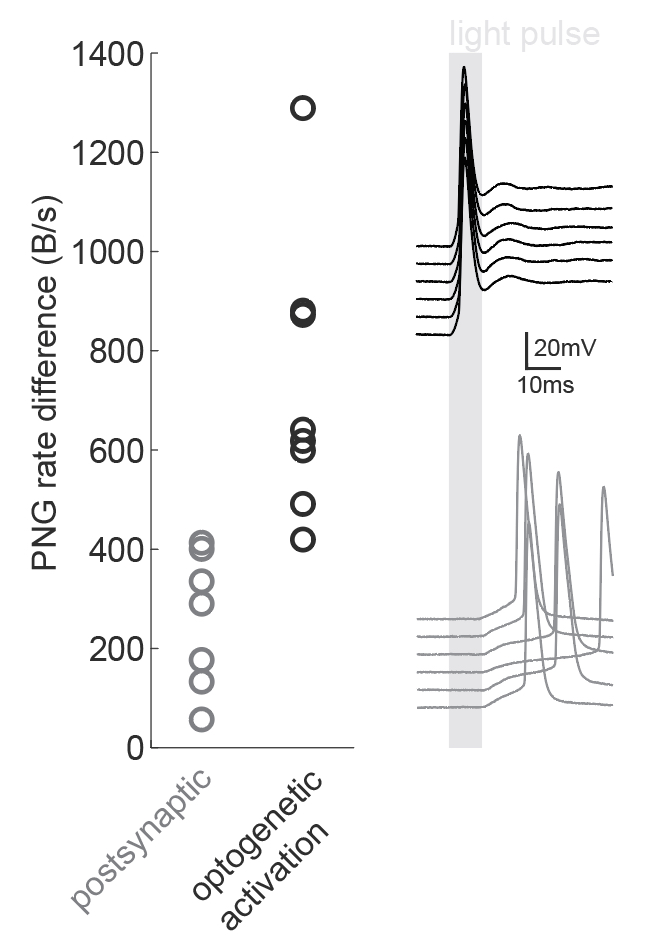
Figure caption: Using a PNG entropy metric to distinguish between direct optogenetic responses and postsynaptic excitatory responses. Left, PNG rate difference calculated for whole cell recordings of optogenetic activation in brain slices. About 20 consecutive 60ms sweeps were analysed from each of 7 postsynaptic cells and 8 directly activated cells. Analysis was performed as in Fig4B of the preprint (https://doi.org/10.1101/2020.08.04.236174) using code from https://github.com/Sylvain-Deposit/PNG-Entropy/blob/master/BatchSaveAsPNG.py. Right, six example traces from a cell carrying channelrhodopsin (black, top) and a cell that was excited synaptically (gray, bottom).
References
Ince, R.A.A., Mazzoni, A., Petersen, R.S., and Panzeri, S. (2010). Open source tools for the information theoretic analysis of neural data. Front Neurosci 4. https://doi.org/10.3389/neuro.01.011.2010
O'Keefe, J., & Dostrovsky, J. (1971). The hippocampus as a spatial map. Preliminary evidence from unit activity in the freely-moving rat. Brain Research, 34(1), 171-175. https://doi.org/10.1016/0006-8993(71)90358-1
Skaggs, M. E., McNaughton, B. L., Gothard, K. M., and Markus, E. J. (1993). An information-theoretic approach to deciphering the hippocampal code. Adv. Neural Inform. Process Syst. 5, 1030-1037.
Tovée, M.J., Rolls, E.T., Treves, A., and Bellis, R.P. (1993). Information encoding and the responses of single neurons in the primate temporal visual cortex. J Neurophysiol 70, 640-654. https://doi.org/10.1152/jn.1993.70.2.640
Treves, A., and Panzeri, S. (1995). The Upward Bias in Measures of Information Derived from Limited Data Samples. Neural Computation 7, 399-407. https://doi.org/10.1162/neco.1995.7.2.399
Verdú, S. (2019). Empirical Estimation of Information Measures: A Literature Guide. Entropy (Basel) 21. https://doi.org/10.3390/e21080720
Wagstaff, K.L., and Corsetti, F.A. (2010). An evaluation of information-theoretic methods for detecting structural microbial biosignatures. Astrobiology 10, 363-379. https://doi.org/10.1089/ast.2008.0301
Yuste, R., Hawrylycz, M., Aalling, N., Aguilar-Valles, A., Arendt, D., Armañanzas, R., Ascoli, G.A., Bielza, C., Bokharaie, V., Bergmann, T.B., et al. (2020). A community-based transcriptomics classification and nomenclature of neocortical cell types. Nat Neurosci 23, 1456-1468. https://doi.org/10.1038/s41593-020-0685-8
Zbili, M., and Rama, S. (2021). A quick and easy way to estimate entropy and mutual information for neuroscience. BioRxiv 2020.08.04.236174. https://doi.org/10.1101/2020.08.04.236174
The recommender in charge of the evaluation of the article and the reviewers declared that they have no conflict of interest (as defined in the code of conduct of PCI) with the authors or with the content of the article. The authors declared that they comply with the PCI rule of having no financial conflicts of interest in relation to the content of the article.
Reviewed by Federico Stella, 16 Mar 2021
The authors answered my concerns and I think the paper does not need further additions.
Reviewed by anonymous reviewer 1, 28 Feb 2021
The second submission version of the manuscript addresses most of the remarks that I made in the previous round. I appreaciate also the additions included in the new version, namely the introduction of the smart PNG-rate concept, and the new possible application examples. However, some of the issues I pointed out about the original version have not been dealt with completely, and would still need minor revision.
The main remark is still about the definitions and terminology. The authors have clarified the presentation and use of the terms well, but I still find that there are a few more clarifications needed.
For one, the concept of entropy rate still pops up out of the blue in the presentation. It appears first on line 86, then on lines 141-142, and then in Section 2.2. It should preferably be defined before all of these in a formal way. A somewhat formal definition is given on lines 247-248 with "The entropy rate R is defined as $R = \frac{1}{T}H$ with T being the sampling of the signal." This should indeed appear earlier, with also preferably a bit of more elaboration.
Moreover, the term 'sampling of the signal' for $T$ in the above quote is inconsistent with the earlier terminology. Also, I still hope for more clarification of the term 'size'. This also applies to its use on lines 84-86; i.e. what does "a signal of size S" exactly mean?
In addition, I still find a few smaller remarks about the manuscript. The authors have dealt only partly with my remark about italicization of math symbols. For instance, around Equation 1, the $xi$-terms are only in italic in the equation, but not in the body text. The symbols should be in italic everywhere, not only inside equations. This should also apply also to the variables $T$, $v$, $RS$, $R_N$, the probabilities $p(x)$, etc.
There still appear some language issues and typos, e.g. two in "In this study, the authors showed that a larger synapse drived the postsynaptic spiking in a greater manner, which increase the SIE." At least some of these mistakes should be possible to detect even with proof-reading software. Correcting them would make the presentation more convincing and readable.
Evaluation round #1
DOI or URL of the preprint: 10.1101/2020.08.04.236174
Version of the preprint: 1
Author's Reply, 31 Jan 2021
Decision by Haudur Freyja Olafsdottir, Mahesh Karnani and Fleur Zeldenrust, posted 05 Nov 2020
and Fleur Zeldenrust, posted 05 Nov 2020
Dear Sylvain and Mickael, Thanks for submitting your preprint to PCI C Neuro, and apologies again for the delays - it took us some time to reach outside our usual neuroscientist pool in order to get feedback on the mathematics as well. The reviews of your manuscript "A quick and easy way to estimate entropy and mutual information for neuroscience" are below. The manuscript was evaluated by 2 reviewers and 2 of us (reviewers 3 and 4). Everyone was enthusiastic about the work, but felt there were some crucial edits to be made. Furthermore, the reviewers would like you to make explicit under what experimental conditions the method can be used, which could enhance the use of the presented method. If you could write a response to the reviews and upload a revised preprint, we would be happy to evaluate a revision for recommendation, this time with a much faster turnaround time. We hope this feedback helps in the preparation of a revised manuscript. Thank you for participating in the PCI Circuit Neuroscience initiative. Best regards, Freyja, Mahesh and Fleur Reviewer 1: The manuscript presents a novel method for entropy estimation based on leveraging on optimal noiseless compression algorithms, already developed for image processing, and in particular on the PNG format. The idea is that the size of the PNG file obtained by saving a particular set of data will reflect the amount of variability present in the data and will therefore provide with an indirect estimation of the entropy content of the data. The method is based on Shannon’s Source Coding Theorem, therefore approaching entropy estimation problem from the field of compressed sensing, something that as the authors rightly state, has not yet found wide use at least in the field of neuroscience. The resulting algorithm is extremely straightforward, essentially consisting in just the PNG saving step. Therefore it provides a useful tool for a fast and computationally efficient evaluation of the complexity of a signal, without having to resort to more math-heavy methods (as the math is done “for free” by the PNG compression software). The main issue with this method is that in its present form is essentially limited to a private use by the experimenter, when needing to have a on-the-go assessment of the variation of entropy content in some preparation. Especially, it seems to me that it is particularly suitable for well controlled recordings with multiple trials of fixed length or for continuous imaging of cell cultures (and indeed, these are the examples presented in the manuscript). It would problematic to apply the method in its present form either to experiments with a larger behavioral component or, on the other hand, to compare different recordings This comes from the fact that the PNG conversion method presented here allows only for relative entropy estimation. The authors rightly note how the size of the file has no direct relationship to the value of entropy. And indeed all the examples presented in the manuscript deal with the estimation of entropy or information content in data of fixed size obtained from the same system. While this is no doubt a very handy approach to obtain quick measures of entropy for large dataset, it is hard for me to see how it could be generalized to allow for comparison across different experimental setup, or the same experimental setup in different conditions. Taking the case of mutual information, consider as an example the mutual information between a place cell activity and the position of the animal in space. The conditional entropy component of the mutual information requires to consider different bins in space, for which variable amount of data would be available, given the heterogeneities of the animal behavior. Moreover comparing two neurons recorded in two different sessions will also present the problem of different exploration time and amount of data. I am not sure wether the authors have already considered cases of this type and wether it would be possible to include a normalization step in their method, so that, for example PNG size is compared to an image of the same size obtained from a random process. As this would greatly extend the applicability of the PNG conversion, the paper would benefit from a discussion of possible solutions to this sort of situation. Reviewer 2: The article proposes quantifying the entropy and mutual information of neuroscientific data based on file size after compressing the data as a PNG-file. The idea is intriguing and is presented and studied in the article fairly thoroughly. The paper has some merits, but there are multiple issues as well, which are listed below. The authors correctly note the issue that file size does not correspond to absolute entropy values. Nevertheless, they state, already in the Abstract, that "we can reliably estimate entropy" with the method, which seems a bit like false advertising. Perhaps using "the level of entropy" in place of just "entropy" would be more accurate. The paper contains some repetition, especially in Sections 2.2 and 3.1. However, even the parts that are explained twice are not explained clearly enough; in particular, the quadratic extrapolation method requires some clarification. The terminology should be defined and stated more clearly and rigorously in the beginning; for instance, the authors use the terms "sampling", "bin" and "word" related to the variable T, but the meaning of these terms and the variable remain nevertheless unclear. The authors state the formula of Shannon entropy in Equation 1, but they do not discuss what is the probability space on which the entropy is considered in the context of the paper. It would be nice to have a discussion about this at least on a descriptive and intuitive level. The authors use the terms entropy and entropy rate in an interchangeable manner, although they are two quite different concepts. Which one are the authors actually interested in computing? This especially causes confusion when interpreting Figure 2A. Figure 2B has a couple of issues: First, the authors state that the plot of the PNG file size "follows the same curve than the entropy". However, although they appear similar, the values of the curves differ quite substantially at ~25% white pixels, where the entropy is around 50% of the maximum entropy but the file size is above 60% of the maximum. Secondly, the file size curve seems slightly asymmetric, which is surprising, as the file size should be the same regardless of whether compressing an image containing x percent white pixels or x percent black pixels. Perhaps the file size curve should be averaged over more runs of the compression? The authors should discuss the fact that, in addition to compression, the PNG algorithm also involves filtering for 2D images, (see e.g. http://www.libpng.org/pub/png/book/chapter09.html ), which affects the compression size of 2D images. The authors should note that this also affects the results gained with the 2D-images. Currently the 2D images are simply transformed into 1D signals. There are quite a few grammatical errors and typos throughout the text, so I would urge the authors to read through and edit the manuscript with care in this respect. The authors talk about "white noise with amplitude x". Is this a common convention for the use of the term amplitude? Perhaps some other terminology would be more standard? The mathematical notation has some issues. Most crucially, Equation 5 for the conditional entropy is simply incorrect. The conditional probability should be denoted with a vertical line "|", not a forward slash "/". The mathematical variables should always be italicized (e.g. on lines 41-42). The two (unnumbered) Equations between lines 161 and 166 are repeated in Equations 2 and 8 unnecessarily. Also, the Equation below line 161 has the term T in all three limits. Reviewer 3: This preprint presents a png-file compression based method for estimating relative entropy of time series signals and 2-d images. The authors start with a very useful presentation of another entropy estimation method and careful demonstration of better performance of the png method. They also explore the limitations in Fig2. After this, they present the use of the png method for analysing neural data by obtaining a metric similar to mutual information for repetitive trials of electrophysiological data, and analysing dendritic complexity in micrographs of neurons. The method appears useful and simple to apply, though parts of the application should be clarified and it would be more useful to present the questions that can be addressed with the method rather than metrics that can be approximated. Only the last use case seems to be addressing a clear question, ‘what is the growth state of a neural culture?’. I have major and minor suggestions for improvement below. Major: 1) Line 296 states that conditional entropy of signal X given signal Y can be interpreted as the noise entropy of X across trials. This seems incorrect and needs justification. Conditional entropy should express the entropy that remains in X given the knowledge of Y. It makes some intuitive sense that the noise entropy of X across trials will be affected by the driving signal Y, but to equate it with conditional entropy as defined in eq.5 seems a step too far. The main usefulness of the png method presented in the paper, estimating mutual information, relies on this interpretation. Perhaps an overly ambitious assumption like this explains the deviations between Fig3C middle and right panels. If the authors could come up with a more convincing method of estimating mutual information with the png approach, that would enhance the usefulness of the paper. However, given that the png method only returns relative entropy of one signal at a time it appears not suited for estimating conditional entropies. Other electrophysiological signal entropy metrics may also be equally useful for the community, such as transfer entropy, and just the relative entropy of signals, but it may be helpful to demonstrate an example of what questions can be answered with these. 2) Entropy of images is presented as another key use of the method in figure 4. The estimation of culture growth stage (Fig4C) is useful. However, the usefulness of the other two presented instances is dubious. Fig4A shows a use in estimating layers in a Cajal drawing. It is unclear why one would need to do this, as the boundaries of layers 2-5 appear to be obscured in the curve, compared to just looking at the drawing. Fig4B shows a use in estimating a curve similar to Sholl analysis (but different enough to not serve the same purpose). As the Sholl analysis curve describes the number of neural branches as a function of radial distance from soma, it gives us an immediately useful metric which needs no interpretation. The png metric however seems more difficult to interpret. It means something about the uncertainty/complexity of dendritic patterns at a given radius. Can the authors explain more why they believe this is useful? Demonstrating an improved identification of cell types based on the png metric over the Sholl curve would make a very strong case for usefulness. As the authors pointed out, astrobiologists can use png metrics to help distinguish between biogenic and nonbiogenic rocks – could the technique offer an equally useful categorization assay for neuroscience? Minor: 1) Authors explain on lines 64-70 that the quadratic extrapolation method is not the only alternative for estimating signal entropy. Why was the quadratic extrapolation method singled out as the comparison for the png method? Would the other methods perform as well or better than the png method? 2) Could the authors mention what computer was used for the study? This is important because, e.g., line 424, it is mentioned that speed is an advantage of the png method because getting the same metric with quadratic extrapolation took 2h. This depends on the hardware. 3) Equation between lines 161 and 162 should be the same as eq.2 on line 222. Reviewer 4: Estimating entropy/mutual information is often a difficult and computationally expensive process, and the simple method the authors propose is attractive, because it offers a quick and easy way to compare the entropy between conditions. However, I think there is an issue, namely that the "file size does not correspond to absolute entropy values", possibly because "the PNG algorithm also involves filtering for 2D images, (see e.g. http://www.libpng.org/pub/png/book/chapter09.html ), which affects the compression size of 2D images". Since entropy and mutual information are almost always heavily dependent on the estimation method (and direct measurement is almost never possible), this is not a problem per se, but I think the authors should be extremely clear on when their method does or does not apply. The authors make strong claims in the abstract ("By simply saving the signal in PNG picture format and measuring the size of the file on the hard drive, we can reliably estimate entropy through different conditions") and although they mention the limitations themselves, both in the abstract and in the text, I think they have to be careful here. So I believe this context should be made clearer, and it should be made explicit when to use (and NOT use) the method. The authors claim in the discussion that "PNG files must be all of the same dimensions, of the same dynamic range and saved with the same software" -- maybe they could think of a few typical experimental conditions where this does or does not apply? Secondly, I also wonder whether the size of a PNG file correlates linearly with the entropy of non-white noise files. The authors do not show this explicitly, only for white nose files, but aren't any signals that we are interested in non-white noise? Finally, personally I would be quite curious where the differences in png file size come from, if it is not the entropy. Do the authors have an opinion on that (because that could help others to judge when or when not one can use the method)?
Reviewed by anonymous reviewer 2, 26 Oct 2020
The manuscript presents a novel method for entropy estimation based on leveraging on optimal noiseless compression algorithms, already developed for image processing, and in particular on the PNG format. The idea is that the size of the PNG file obtained by saving a particular set of data will reflect the amount of variability present in the data and will therefore provide with an indirect estimation of the entropy content of the data. The method is based on Shannon’s Source Coding Theorem, therefore approaching entropy estimation problem from the field of compressed sensing, something that as the authors rightly state, has not yet found wide use at least in the field of neuroscience. The resulting algorithm is extremely straightforward, essentially consisting in just the PNG saving step. Therefore it provides a useful tool for a fast and computationally efficient evaluation of the complexity of a signal, without having to resort to more math-heavy methods (as the math is done “for free” by the PNG compression software).
The main issue with this method is that in its present form is essentially limited to a private use by the experimenter, when needing to have a on-the-go assessment of the variation of entropy content in some preparation. Especially, it seems to me that it is particularly suitable for well controlled recordings with multiple trials of fixed length or for continuous imaging of cell cultures (and indeed, these are the examples presented in the manuscript). It would problematic to apply the method in its present form either to experiments with a larger behavioral component or, on the other hand, to compare different recordings
This comes from the fact that the PNG conversion method presented here allows only for relative entropy estimation. The authors rightly note how the size of the file has no direct relationship to the value of entropy. And indeed all the examples presented in the manuscript deal with the estimation of entropy or information content in data of fixed size obtained from the same system. While this is no doubt a very handy approach to obtain quick measures of entropy for large dataset, it is hard for me to see how it could be generalized to allow for comparison across different experimental setup, or the same experimental setup in different conditions.
Taking the case of mutual information, consider as an example the mutual information between a place cell activity and the position of the animal in space. The conditional entropy component of the mutual information requires to consider different bins in space, for which variable amount of data would be available, given the heterogeneities of the animal behavior. Moreover comparing two neurons recorded in two different sessions will also present the problem of different exploration time and amount of data. I am not sure wether the authors have already considered cases of this type and wether it would be possible to include a normalization step in their method, so that, for example PNG size is compared to an image of the same size obtained from a random process. As this would greatly extend the applicability of the PNG conversion, the paper would benefit from a discussion of possible solutions to this sort of situation.
Reviewed by anonymous reviewer 1, 29 Sep 2020
The article proposes quantifying the entropy and mutual information of neuroscientific data based on file size after compressing the data as a PNG-file. The idea is intriguing and is presented and studied in the article fairly thoroughly. The paper has some merits, but there are multiple issues as well, which are listed below.
The authors correctly note the issue that file size does not correspond to absolute entropy values. Nevertheless, they state, already in the Abstract, that "we can reliably estimate entropy" with the method, which seems a bit like false advertising. Perhaps using "the level of entropy" in place of just "entropy" would be more accurate.
The paper contains some repetition, especially in Sections 2.2 and 3.1. However, even the parts that are explained twice are not explained clearly enough; in particular, the quadratic extrapolation method requires some clarification. The terminology should be defined and stated more clearly and rigorously in the beginning; for instance, the authors use the terms "sampling", "bin" and "word" related to the variable T, but the meaning of these terms and the variable remain nevertheless unclear.
The authors state the formula of Shannon entropy in Equation 1, but they do not discuss what is the probability space on which the entropy is considered in the context of the paper. It would be nice to have a discussion about this at least on a descriptive and intuitive level.
The authors use the terms entropy and entropy rate in an interchangeable manner, although they are two quite different concepts. Which one are the authors actually interested in computing? This especially causes confusion when interpreting Figure 2A.
Figure 2B has a couple of issues: First, the authors state that the plot of the PNG file size "follows the same curve than the entropy". However, although they appear similar, the values of the curves differ quite substantially at ~25% white pixels, where the entropy is around 50% of the maximum entropy but the file size is above 60% of the maximum. Secondly, the file size curve seems slightly asymmetric, which is surprising, as the file size should be the same regardless of whether compressing an image containing x percent white pixels or x percent black pixels. Perhaps the file size curve should be averaged over more runs of the compression?
The authors should discuss the fact that, in addition to compression, the PNG algorithm also involves filtering for 2D images, (see e.g. http://www.libpng.org/pub/png/book/chapter09.html ), which affects the compression size of 2D images. The authors should note that this also affects the results gained with the 2D-images. Currently the 2D images are simply transformed into 1D signals, which
There are quite a few grammatical errors and typos throughout the text, so I would urge the authors to read through and edit the manuscript with care in this respect.
The authors talk about "white noise with amplitude x". Is this a common convention for the use of the term amplitude? Perhaps some other terminology would be more standard?
The mathematical notation has some issues. Most crucially, Equation 5 for the conditional entropy is simply incorrect.
The conditional probability should be denoted with a vertical line "|", not a forward slash "/".
The mathematical variables should always be italicized (e.g. on lines 41-42).
The two (unnumbered) Equations between lines 161 and 166 are repeated in Equations 2 and 8 unnecessarily. Also, the Equation below line 161 has the term T in all three limits.










