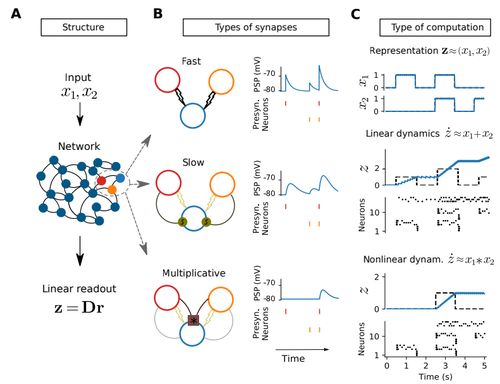
Artificial (spiking) neural networks (ANNs) have become an important tool in the modelling of biological neuronal circuits. However, they come with caveats: their typical training can be laborious, and after it is done, the complexity of the connectivity obtained can be almost as daunting as the original biological systems we are trying to model.

In this work [1], Nardin and colleagues summarize and expand upon the Spike Coding Network (SCN) framework [2], which originally provides a direct method to derive the connectivity of a spiking ANN representing any given linear system. They generalize this framework to approximate any (non-linear) dynamical system, by yielding the connectivity necessary to represent its polynomial expansion. This is achieved by including multiplicative synapses in their network connections. They show that higher polynomial orders can be efficiently represented with hierarchical network structures. The resulting networks not only enjoy many of the desirable features of traditional ANNs, like robustness to (artificial) cell death and realistic patterns of activity, but also a much more interpretable connectivity. This is promptly leveraged to derive how densely connected a neural network of this type needs to be to be able to represent dynamical systems of different complexities.

The derivations in this work are self-contained and the mathematically inclined neuroscientist can quickly get up to speed with the new multiplicative SCN framework, without the need for prior specific knowledge of SCNs. All the code is available and well commented in https://github.com/michnard/mult_synapses making this introduction even more accessible to its readers. This paper is relevant for those interested in neural representations of dynamical systems and the possible roles for multiplicative synapses and dendritic non-linearities. Those interested in neuromorphic computations will find here an efficient and direct way of representing non-linear dynamical systems (at least those well approximated by low-order polynomials). Finally, those interested in neural temporal pattern generators might find it surprising that only 10 integrate and fire neurons can already very reasonably approximate a chaotic Lorenz system.

[1] Nardin, M., Phillips, J. W., Podlaski, W. F., and Keemink, S. W. (2021) Nonlinear computations in spiking neural networks through multiplicative synapses. arXiv, ver. 4 peer-reviewed and recommended by Peer Community in Neuroscience. https://arxiv.org/abs/2009.03857v4

[2] Boerlin, M., Machens, C. K., and Denève, S. (2013). Predictive coding of dynamical variables in
balanced spiking networks. PLoS Comput Biol, 9(11):e1003258. https://doi.org/10.1371/journal.pcbi.1003258