
Approximate any nonlinear system with spiking artificial neural networks: no training required
Nonlinear computations in spiking neural networks through multiplicative synapses
Abstract
Recommendation: posted 25 November 2021, validated 29 November 2021
Leite, M. (2021) Approximate any nonlinear system with spiking artificial neural networks: no training required. Peer Community in Neuroscience, 100003. 10.24072/pci.cneuro.100003
Recommendation
Artificial (spiking) neural networks (ANNs) have become an important tool in the modelling of biological neuronal circuits. However, they come with caveats: their typical training can be laborious, and after it is done, the complexity of the connectivity obtained can be almost as daunting as the original biological systems we are trying to model.
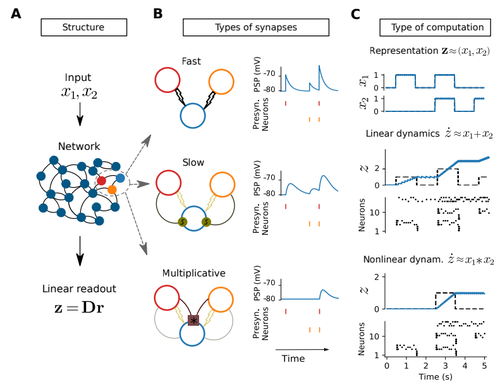
In this work [1], Nardin and colleagues summarize and expand upon the Spike Coding Network (SCN) framework [2], which originally provides a direct method to derive the connectivity of a spiking ANN representing any given linear system. They generalize this framework to approximate any (non-linear) dynamical system, by yielding the connectivity necessary to represent its polynomial expansion. This is achieved by including multiplicative synapses in their network connections. They show that higher polynomial orders can be efficiently represented with hierarchical network structures. The resulting networks not only enjoy many of the desirable features of traditional ANNs, like robustness to (artificial) cell death and realistic patterns of activity, but also a much more interpretable connectivity. This is promptly leveraged to derive how densely connected a neural network of this type needs to be to be able to represent dynamical systems of different complexities.
The derivations in this work are self-contained and the mathematically inclined neuroscientist can quickly get up to speed with the new multiplicative SCN framework, without the need for prior specific knowledge of SCNs. All the code is available and well commented in https://github.com/michnard/mult_synapses making this introduction even more accessible to its readers. This paper is relevant for those interested in neural representations of dynamical systems and the possible roles for multiplicative synapses and dendritic non-linearities. Those interested in neuromorphic computations will find here an efficient and direct way of representing non-linear dynamical systems (at least those well approximated by low-order polynomials). Finally, those interested in neural temporal pattern generators might find it surprising that only 10 integrate and fire neurons can already very reasonably approximate a chaotic Lorenz system.
[1] Nardin, M., Phillips, J. W., Podlaski, W. F., and Keemink, S. W. (2021) Nonlinear computations in spiking neural networks through multiplicative synapses. arXiv, ver. 4 peer-reviewed and recommended by Peer Community in Neuroscience. https://arxiv.org/abs/2009.03857v4
[2] Boerlin, M., Machens, C. K., and Denève, S. (2013). Predictive coding of dynamical variables in
balanced spiking networks. PLoS Comput Biol, 9(11):e1003258. https://doi.org/10.1371/journal.pcbi.1003258
The recommender in charge of the evaluation of the article and the reviewers declared that they have no conflict of interest (as defined in the code of conduct of PCI) with the authors or with the content of the article. The authors declared that they comply with the PCI rule of having no financial conflicts of interest in relation to the content of the article.
SWK was supported by the Simons Collaboration on the Global Brain (543009). WFP was supported by FCT (032077). MN was supported by European Union Horizon 2020 (665385).
Evaluation round #2
DOI or URL of the preprint: https://arxiv.org/abs/2009.03857v3
Version of the preprint: v3
Author's Reply, 22 Nov 2021
Dear Marco Leite,
thanks again for reviewing our paper, and no worries regarding the delay. We are happy that the new version has improved and happy that it will be recommended once we settle the last details. Here are our responses to the minor points raised:
1) In section 5, in the new added text you write: "we have considered that each neuron codes for each dimension", while my understanding is that it should read "we have considered that each neuron codes for all dimensions", is this correct?
This is correct. Changing the sentence "we have considered that each neuron codes for each dimension" --> "we have considered that each neuron codes for all dimensions" is indeed what we meant, and the new phrasing is better and less confusing.
2) The GitHub repository is missing the code for figure 4 and for the supplementary figures as well, it would be important to have them for completeness and reproducibility.
We will add the remaining code to Github by the end of this week.
We thank you again for the time put into this review, and thank the entire PCI community.
Kind regards,
Michele Nardin, James Phillips, William Podlaski & Sander Keemink
Decision by Marco Leite, posted 05 Nov 2021
Dear Authors,
Thank you for your patience regarding the recommendation process, in normal circumstances it should not take this much time, and I apologize for that.
I am raising only a couple of minor points that need your attention:
- In section 5, in the new added text you write: "we have considered that each neuron codes for each dimension", while my understanding is that it should read "we have considered that each neuron codes for all dimensions", is this correct?
- The GitHub repository is missing the code for figure 4 and for the supplementary figures as well, it would be important to have them for completeness and reproducibility.
Once these are addressed I will be very happy to publish the my already prepared recommendation.
Kind regards,
Evaluation round #1
DOI or URL of the preprint: https://arxiv.org/abs/2009.03857v2
Author's Reply, 04 Aug 2021
Decision by Marco Leite, posted 14 Jun 2021
Dear Michele Nardin,
Once again thank you for submiting your preprint for review in PCI C Neuro. We have gathererd the opinion of two reviewers and feel that the preprint represents a substantial contribution for the field of spiking neural networks. However, before proceeding with a recomendation, the reviewers have several comments that require your attention. Please consider addressing these point by point and submiting a revised version of the manuscript.
Kind regards,
Marco Leite
Reviewed by anonymous reviewer 2, 04 May 2021
Overall, I like the paper very much. I think it is a very nice extension of the SCN framework. The maths is thorough and the paper is written clearly (although a few clarifications are necessary).
Most of my criticism revolves around the lack of a clear biological mechanism behind multiplicative synapses. Even though it is not strictly necessary that the authors deliver a precise biological interpretation, the paper could benefit from a more detailed examination of possibilities. It would moreover strengthen the validity of multiplicative synapses.
Major
- I am still struggling to think of an implementation of multiplicative synapses that is biologically feasible. For example, in 1B last row, how would the blue neuron know about the coincident firing of red and orange? In this simple illustration, one might think that a simple spiking threshold could do the trick. Basically, only when two neurons are activated at the same time, blue reaches the threshold. However, I am not sure if this interpretation can be generalized easily. If so, it would make strong predictions about spiking thresholds etc. Anyway, it would be nice if the authors could go more into the details how neurons can implement the multiplicative synapses (The authors state in the Methods „[…] each neuron in Gd needs to keep track of coincident firing of any neuron in Ge with any other in Gf.“ And I think it would be nice to have a clearer picture of how this can be achieved in biological systems)
- 4.2: To prove that higher-order multiplicative synapses are not strictly necessary, you stack two networks together that can compute third-order multiplications with pairwise interactions.
- I think this would make strong predictions about the brain’s connectivity structure that might be visible in one way or another. Is there evidence for such a hypothesis?
- In the example you show, there is no difference between triplet and no triplet suggesting that both have the very same performance. However, I guess there are examples where the triplet (or even higher-order multiplicative synapse) is necessary to achieve a reasonable performance. It would be nice if this could be discussed more so that the reader gets a better understanding of the limitations
- Section 5 needs clarification: This section is very important but is not explained well (I feel it should be extended significantly).
- Also, Fig. 4 is not completely clear. Dashed lines are derived from theory!? Refer to the eq. In the methods section. Solid lines are mean derived from the simulations?
- It would be nice to show performances (maybe for the example shown before) in the case when no one-to-one connectivity is used. This would make it easier for the reader to evaluate how well the approach works even in more biologically plausible regimes
- The authors use phrases like „signal dimensions“ or „dynamical system density“ for the very first time in section 5. Even though it becomes clear over time, it would be nice, if these terms could be introduced properly.
Minor
- In abstract: „Synapse type“. For readers that are not familiar with SCN, this might be misleading. They could think of excitatory vs. inhibitory, and not fast, slow etc. as you have in mind
- Page 3, (b): „iff“
- The last row in Fig. 1B is very nice, but to make sure that the reader does understand the general concept, an illustration beyond m=2 could be helpful.
- Page 5: you reference to Fig. 1C, D —> there is no D
- Page 6: your reference to Fig. 2Aiii (see second paragraph, end) but mean 2Aiv
- Page 6: your reference to Fig. 2Biii (see third paragraph, middle) but mean ii
- Below Eq. 7 —> could you please briefly state how you ended up with equation (log2(g)-1) support networks
- Page 10 (before Discussion): You refer to FIg. 3 but mean Fig. 4
- In Eq. (8): Is the Heaviside step function hidden in the sum (the exponentials should not have an impact before the spike was emitted) … sorry it is late and I am tired. ;)
- Before Eq. (14) in the text: should be - D_i^T y = … )
- Before 7.3: You refer to Supp. Fig. 1 but you mean 2
- You introduce the Kroneker product on page 16 but it has been used throughout the Methods section. It would make sense to restructure the Methods part and introduce this important concept before
- First line page 17: the
- Before Eq. 23: double the
- Method section 7.7 needs more clarification (and please also use equation numbers here). Especially, the equations E(F), E(S), and E(Q) need more explanations.
Reviewed by anonymous reviewer 1, 02 Jun 2021
In this manuscript, the authors provide an important theoretical contribution to the understanding of spiking neural networks, by describing mathematically how to design neural networks to implement any type of polynomial dynamics. The study is based on previous work on the spike coding framework (Boerlin et al. 2013), initially based on generating linear dynamical systems, that has been then extended in several publications to account for different biological constraints and non-linear dynamics. In this study, the authors explore an alternative top-down extension of the framework to generate non-linear dynamics based on multiplicative synapses. After defining the mathematical framework, the study illustrates the application of the method to a standard benchmark: the chaotic dynamics of a Lorenz attractor. Next, they show an alternative implementation, based on a hierarchical multi-network architecture, that can implement polynomial dynamics using only pairwise multiplicative synapses. Finally, they consider how the top-down assumptions of the model relate to biological constraints in brain wiring, and compare their advantages and disadvantages with respect to other existing methods. This effort in the discussion is necessary, since how is the main premise of this theoretical work -multiplicative synapses- remains an open question.
This work is quite technical, and builds on previous theoretical work. Nevertheless, the authors make an effort to explain previous findings and make this study accessible to readers familiar with standard methods in computational neuroscience methods, but not necessarily with the spike coding framework. The findings of the study constitute a solid advancement in the understanding of computations in spiking networks, and open new paths for potential impactful applications in the field.
Comments
Introduction
In the second sentence of the first paragraph, it remains unclear to me why the implementation of non-linear dynamics through the recurrent connectivity, leads to (“accordingly”) low-dimensional internal representations. I believe this statement makes sense based on the assumption that the implemented non-linear dynamics are low-dimensional. If this is the case, I would suggest to specify it. Otherwise, these two ideas (non-linear computation implemented by recurrent wiring and low-dimensional representations) should be presented separately.
2 Spike coding networks
It seems thet there are missing references to some of the panels in Fig 1 in the main text (check as well for other figures). Fig 1A for example is not referred to anywhere. It could be included in Section 2.1.
In Section 2.2, I suggest to give a more precise intuition about why and what is “fast” in fast connections and what is “slow” in slow connections. Although this terminology is commonly used in the spike coding framework, it would help understanding the difference between Fig 1B top and middle, which is currently not commented in the main text.
If I understood correctly, the middle row in Fig 1B+C has both fast and slow synapses.
Also, there is no reference to Fig1C middle in section 2.2.
3 Nonlinear dynamics
In Section 2.3, I suggest highlighting the fact that the Lorenz attractor is based on pairwise multiplications of the state-variables, since this concept is useful for the rest of the paper.
4 Higher-order polynomials
Reference to the Supp. Fig. 2 needs more context. Since Supp. Fig 2 does not show any combination of networks, it is worth explaining in a sentence why it is relevant here.
In Section 4.3 and corresponding Fig. 3, it remains unclear whether the double pendulum implementation corresponds to the approximated dynamics (where sin theta = theta) for all lines, or whether this approximation is used only for the spike coding networks.
5 On the number of required connections
It is currently hard to understand this section and the content of Fig. 6, just by reading the caption and the main text, without looking at the methods. Some sentences would require more explanations (“The fast connections only depend on the density of the decoder, and any two neurons are connected whenever they share a decoding-dimension”). I suggest moving part of the Methods 7.7 into the main text.
Discussion
Section 6.2
Reference to Fig. 3 should be Fig. 4, I believe.
Methods
I suggest including Section 7.3 before Section 7.2. The Kronecker product is first explained in Section 7.3, although already used in Section 7.2. Explain what Section 7.2 wants to calculate before starting calculating (introduce matrix W, for example). included before S the Methods. In
Misc errors
- I believe matrix D should be in bold in Eq. 3
The colors of the two neurons in Figure 1 look to me red and orange, instead of red and green as indicated in the caption.
Section 3.1: Reference to Fig. 2Aiii at the end of the second paragraph should actually be Fig. 2A iv ?
Section 3.1: the network simulation still display the… -> the network simulation still displays the
Section 3.1: (Fig. 2top) -> (Fig. 2 top)
Section 3.2: high pair-wise connectivity -> dense pair-wise connectivity? high-density pair-wise connectivity?
Methods 7.3: “among the other properties, the one that will be used is…”-> (suggestion) We use the mixed-product property
Methods 7.5: nonliarity -> non-linearity or nonlinearity
Methods 7.7.2: the second part-> the second term.
So the interesting part is… -> We focus on the first term …










